|
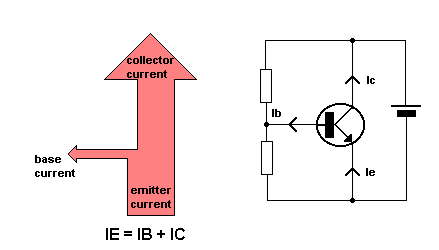
The forward biased base/emitter junction causes electrons to be attracted from
the emitter area towards the base. Arriving in the base area, most of the
negative electrons come under the influence of the more positive collector and
are attracted by it. This is shown in the left hand drawing, where the base
current plus collector current equals the emitter current. Alpha gain is
collector current divided by emitter current, and is always less than 1. Beta
gain is collector current divided by base current and can be a fairly high
number. Therefore, causing a small base current to flow makes a much larger
collector current flow. A small base current controls a large collector current.
There is 0.6 volts across the base/emitter junction, when it is forward biased.
(0.3 volts for germanium). |