|
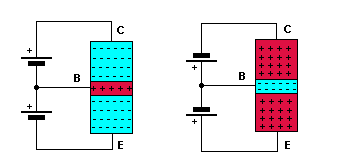
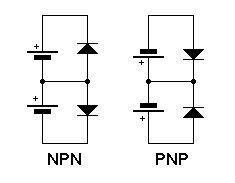
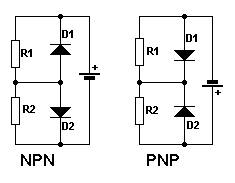
The emitter/base junction is forward biased. The collector/base junction is reversed biased. There is an explanation of biasing on one of the diode junction pages. The middle diagram shows the two junctions as two diodes. Ofcourse, you can't make a transistor like this but it helps to understand the forward and reverse biasing. The anodes are positive with respect the cathodes for forward biasing. They are negative with respect to the cathodes for reverse biasing. The diagram shows the junctions being correctly biased using just one battery.
Note that there is 0.6 volts across the base/emitter junction when it is forward
biased, for a silicon transistor. (0.3 volts for a germanium one). |