|
Read the page on
potential dividers. In Fig.1, the 15 volts
will be divided across
the two resistors,
according their
proportion of the total
resistance, 15k.
For the 5k this will be
(5k/15k) x 15volts =
5volts.
For the 10k it will be
(10k/15k) x 15 volts =
10 volts
In Fig.2 we have the
same potential divider
plus R3 and R4 across
the battery. This is a
BRIDGE circuit ,
invented by Mr.
Wheatstone.
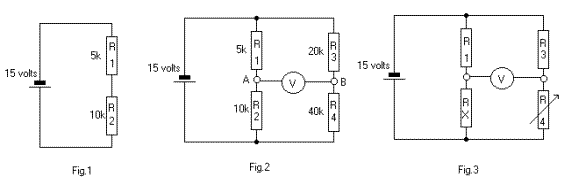 Using the same
calculations as for R1
and R2, we find that the
voltage across R3 = 5
volts and across R4 = 10
volts.
The voltage has been
divided in the same
proportions.
This is because the
ratio R1/R2 is the same
as the ratio R3/R4, that
is, 1:2.
The meter, connected
between points A and B
will indicate zero.
This is because the
voltage at both
terminals of the meter
is the same, so the
voltage across the meter
is zero.
The bridge is said to be
BALANCED.
So we can say that when
the ratio R1/R2 = R3/R4,
the bridge is balanced.
If the two ratios are
not the same, then the
voltages at the two
terminals of the meter
will be different.
The meter will now give
a reading, and we can
say that the bridge is
unbalanced.In Fig.3, Rx is of
unknown value and the
probability is that the
bridge is unbalanced,
indicated by a reading
on the meter.
If we adjust R4 so that
the ratio R1/Rx = R3/R4
then the bridge will be
balanced.
If we transpose this
equation we can get Rx =
(R4 xR1)/R3
We know the values of R1
and R3.
If we measure the value
of R4 we can calculate
the unknown Rx.
R4 can be fitted with a
pointer and a calibrated
scale to give a direct
reading of Rx without
the need for
calculations.
This is the basis of
more complex bridge
circuits. |