Friction and the Dead Zone

The torque versus position curve shown in Figure 2.1 does not take into account the torque the motor must exert to overcome friction! Note that frictional forces may be divided into two large categories, static or sliding friction, which requires a constant torque to overcome, regardless of velocity, and dynamic friction or viscous drag, which offers a resistance that varies with velocity. Here, we are concerned with the impact of static friction. Suppose the torque needed to overcome the static friction on the driven system is 1/2 the peak torque of the motor, as illustrated in Figure 2.4.

Figure 2.4

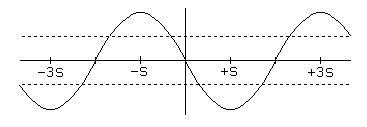
The dotted lines in Figure 2.4 show the torque needed to overcome friction; only that part of the torque curve outside the dotted lines is available to move the rotor. The curve showing the available torque as a function of shaft angle is the difference between these curves, as shown in Figure 2.5:

Figure 2.5

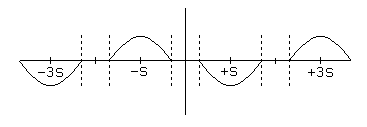
Note that the consequences of static friction are twofold. First, the total torque available to move the load is reduced, and second, there is a dead zone about each of the equilibria of the ideal motor. If the motor rotor is positioned anywhere within the dead zone for the current equilibrium position, the frictional torque will exceed the torque applied by the motor windings, and the rotor will not move. Assuming an ideal sinusoidal torque versus position curve in the absence of friction, the angular width of these dead zones will be:

d = 2 ( S / ( /2) ) arcsin( f / h ) = ( S / ( /4) ) arcsin( f / h )

d -- width of dead zone, in radians

S -- step angle, in radians

f -- torque needed to overcome static friction

h -- holding torque

The important thing to note about the dead zone is that it limits the ultimate positioning accuracy! For the example, where the static friction is 1/2 the peak torque, a 90° per step motor will have dead-zones 60° wide! That means that successive steps may be as large as 150° and as small as 30°, depending on where in the dead zone the rotor stops after each step!

The presence of a dead zone has a significant impact on the utility of microstepping! If the dead zone is x° wide, then microstepping with a step size smaller than x° may not move the rotor at all. Thus, for systems intended to use high resolution micro stepping, it is very important to minimize static friction.